General Report on Tunny
11B Page 8
(g) Limitations.
The sequence of characters defined in paragraph (f) as the LIMITATION is a byproduct of the other patterns on the machine or in the P-stream, and is not generated independently. Four different methods have been used to produce the limitation and the four different types are defined as follows:
(i) Χ2 limitation (known for short as Χ2 lim. or chi 2 lim).
The active character of the limitation at any position is given by the character of Χ2 which was active in the previous position. This is called chi 2 ONE BACK and written Χ2.
(NB Χ2
means Χ2 two back, Χ2 means Χ2
one forward etc.)
(ii) Χ2 + Ψ1' limitation (known for short as Ψ1 lim or Psi 1 lim).
The active character of the limitation is given by the sum of the characters of Χ2 and Ψ'1 which were active in the previous position.
(iii) Χ2 + P5 limitation (known for short as P5 lim.)
The active character of the limitation is given by the sum of the character of Χ2 which was active in the previous position and the character of P5 which was active two positions previously.
(iv) Χ2 + Ψ'1 + P5 (known for short as Ψ1, P5 lim.)
The active character of the limitation is given by the sum of the characters of Χ2 and Ψ'1 which were active in the previous position and the character of P5 which was active two positions previously.
Limitations involving P5 constitute an "autoclave" since the key stream becomes dependent on the Plain Language.
On the earliest model of the Tunny machine there was "No limitation". This was equivalent to a limitation stream consisting entirely of crosses, so that Total and Basic motors were the same.
(h) A General Example of Ciphering with Χ2 + Ψ1' limitation.
| (i) | P: | 9 I M 9 K A M P F 9 G E G E N 9 | (given) |
| (ii) | Χ: | U O 8 X X R J Y W O R / E Q L 3 | (given) |
| (iii) | Ψ: | N L D E Q / K H B 4 | (given) |
| (iv) | BM: | . . x x . . x . x . x x . . . x | (given) |
| (v) | Χ2: | x . x . . x x . x . x . . x x . | (from ii) |
| (vi) | Χ2 + Ψ'1: | x . x x x . . x x x . . x x x . | (from v and x) |
| (vii) | Χ2 + Ψ'1 | . x . x x x . . x x x . . x x x | (from vi) |
| (viii) | TM: | x . x x . . x x x . x x x . . x | (from iv and vii) |
| (ix) | Ψ': | N L L D E E E Q / K K H B 4 4 4 | (from iii and viii) |
| (x) | Ψ'1: | . . . x x x x x . x x . x . . . | (from ix) |
| (xi) | K = Χ + Ψ': | J R F H M J R 4 W Q S H C Y T R | (from ii and ix) |
| (xiii) | Z = P + K: | K N Z T W 3 P H V W 8 Y 4 H M C | (from i and xi) |
Note that the Ψ' (ix) depends on (vi) which depends on a character in Ψ' at a previous place. Ψ' therefore depends on its own recent past and can only be constructed letter by letter. Only when the 4th letter of Ψ' is known can we tell if there is an extension in the Ψ from the 5th letter to the 6th, and so determine the 6th letter for certain. When this is known, and only then, can we start to find out if the Ψ is extended from the 7th to the 8th letters, and so on.
The underlinings in the example show the relation between Total Motor dots and psi extensions.
(i) Functional Summary.
The action of the Tunny machine at any given position is most easily expressed by the formula
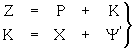 |
(A2) |
Back to General Report on Tunny. Contents.