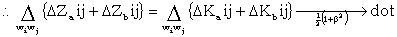General Report on Tunny
22W Page 73
If  is a letter of n dots and m crosses
is a letter of n dots and m crosses
P(ΔΨ'a + ΔΨ'b =  | TMa = ., TMb = .) = | TMa = ., TMb = .) =  = = |
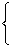 |
1, m = 0 |
(W1) |
| 0, m ≠ 0 |
P(ΔΨ'a + ΔΨ'b =  | TMa = ., TMb = x) = | TMa = ., TMb = x) =  = = |
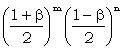 |
(W2) |
P(ΔΨ'a + ΔΨ'b =  | TMa = x, TMb = x) = | TMa = x, TMb = x) = 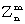 = = |
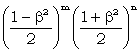 |
(W3) |
and P(ΔΨ'a + ΔΨ'b =  ) = ) = |
(1 - a)2 + 2a(1 - a) + 2a(1 - a) + a2 + a2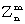 |
|
| = |
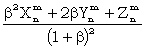 |
(W4) |
Because limitation (L) is equivalent to ΔΨ'b + x,
P(ΔΨ'a + ΔΨ'b =  | La + Lb = .) = | La + Lb = .) = |
P(ΔΨ'a +ΔΨ'b =  | P(ΔΨ'a +ΔΨ'b = | P(ΔΨ'a +ΔΨ'b =  ) ) |
| = |
 |
|
| = |
2P(ΔΨ'a +ΔΨ'b =  ) ) |
(W5) |
Similarly P(ΔΨ'a + ΔΨ'b =  | La + Lb = x) = 2P(ΔΨ'a +ΔΨ'b = | La + Lb = x) = 2P(ΔΨ'a +ΔΨ'b =  ) ) |
(W6) |
The following table (for m + n = 5) is constructed, with the aid of W1, 2, 3, 4, 5, 6, in the same way as the table in the last section and gives deciban scores per letter and is used for scoring possible positions for go-backs. Scores for intermediate dottages can be interpolated.
| |
La + Lb = dot |
La + Lb = cross |
Dottages |
| 15 | 18 | 21 | 24 | 27 |
| Number of dots(n) |
|
|
|
|
|
|
|
Fig. (XV)
(c) The sum of two key streams.
It has been suggested that in cases where there are two stretches of Z with the same P it might be possible to find the relative positions of the P, even if neither messages has been decoded for ΔZa + ΔZb = ΔKa + ΔKb
| |
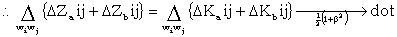 |
(W8) |
< previous
next >
Back to General Report on Tunny. Contents.
Back to The Enigma and the Bombe main page
Home
 is a letter of n dots and m crosses
is a letter of n dots and m crosses
 | TMa = ., TMb = .) =
| TMa = ., TMb = .) =  =
= 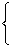
 | TMa = ., TMb = x) =
| TMa = ., TMb = x) =  =
= 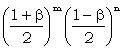
 | TMa = x, TMb = x) =
| TMa = x, TMb = x) = 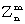 =
= 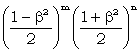
 ) =
) =  + 2a(1 - a)
+ 2a(1 - a) + a2
+ a2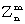
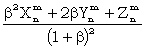
 | La + Lb = .) =
| La + Lb = .) = | P(ΔΨ'a +ΔΨ'b =
| P(ΔΨ'a +ΔΨ'b =  )
)
 )
) | La + Lb = x) = 2P(ΔΨ'a +ΔΨ'b =
| La + Lb = x) = 2P(ΔΨ'a +ΔΨ'b =  )
)