General Report on Tunny
23K Page 97
spanning 0001-2002, starting with settings 01, 01, 01, 01, 01 and stepping Χ1, Χ2 together through ten places.
(e) Z Check.
The preliminary checks are described in 35. The text length is measured by hand counter: as soon as the tape is put on Colossus the text length in counted: the score should be one less because of Δ'ing.
(f) D Checks (i.e. check of the D tape made by Tunny).
Two different methods are used
| (i) Comparison of | 
| Δ D 32 letter count using Z-tape and Χ wheels. |
| Δ D 32 letter count using D-tape. |
(ii) On Colossus, using a slide-free portion of text, find the 2nd, 3rd,... 9th letters (by spanning 01-02, 02-03 etc.) and similarly 4 letters at the beginning of each stretch of 620 letters, and the last 4 letters.
Compare this with a print-out, on Junior, of D in widths of 31 (620 = 20 x 31) [For an early form of the test R4 p. 65].
(g) Theory of Χ Test Runs.
Suppose there is one erroneous character in ΔΧi (in fact, if there is one there must be two, because Χi is Δ'd by Colossus). As usual let the text length be N, the wheel length ω.
This one error will cause the score of ΔΧi + U = . to be changed by the excess of dots over crosses in U at the
places against the erroneous character of ΔΧi.
This excess has expected value 0 and standard deviation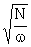 
.
The change will be numerically less than 4 if
 |
|
| If ω = 41, N = 2000, then |sigma-age| < .57 | |
| whose probability is 0 .43 | |
To exclude the possibility of having all changes less then 4 (smaller changes being liable to confusion with unsteady counting by Colossus) a considerable number of readings is required. Ten readings reduce the probability to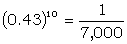 
.
It is clearly wasteful not to include every ΔΧi in every reading taken.
In an archaic version ΔΧ1 + ΔΧi was counted in four positions only: the chance of nearly correct scores with a wrong wheel in the trigger was considerable and is believed to have occurred. [R3 p. 60, 127, 128, 129]
Back to General Report on Tunny. Contents.