General Report on Tunny
23N Page 105
and 3-wheel runs by ordinary long runs. For example the run P3 + P1 = x can be done as a short run (with multiple testing). Or a total motor run can be done instead of a basic motor run (but this cannot be done without multiple testing).
If Χ1 and Χ2 are set a total motor run can be done with a set total of 2σ and then all the results tested out by running P2 + /P1 multiple testing at each motor setting. If Ψ2 has very good slides against itself it is not even necessary to finish the short runs and 20 or 30 different motor settings can be tried out in a few minutes. Another method of doing the total motor run is to do the basic motor run with a set total of 2σ and then run for Ψ1 quintuple testing, but using only counter 1 (the Ψ's corresponding to the other counters are not correctly motorised).
The phenomenon of coalescence occurs with Χ2P5 limitation, this time Ψ5 Corruption is liable to interfere in this case. For further suggestion related to coalescence, see R4 pp. 74, 75, 87, 91, 97, R5 pp. 36, 57, 112.
23P EXAMPLE
For a dossier showing a simple example of a motor and psi run see 23D. For an example showing coalescence see Fig. 23 (I) at the end of this chapter (23).
23W CALCULATION OF THE ODDS OF THE BEST SCORE IN A Χ-SETTING RUN
Suppose we have a message of length N and the score of ΔD1 + ΔD2 = . is ½(N +X) for particular settings of Χ1 and Χ2. Then, as in 24X(e), the factor in favour of these settings is roughly
 |
provided that nothing is known about the scores at other settings. In practice however we do possess additional information. In fact the knowledge which we are usually willing to use in practice is as follows. The bulge of the top score is B1, the bulge of the second best score is B2 and the bulges at all the other settings are (of course) less than B2. Let T1, T2 be the theories that the top score is right or that the second best score is right, respectively, and let T3 be the theory that one of the others is right. The prior probabilities of these theories are respectively,
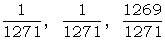. The factors in favour of the first two, not allowing for competition are
 |
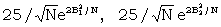In order to obtain the corresponding factor in favour of T3 it is necessary to introduce a new symbol. Let q be the probability that the correct setting will have a bulge less than B2. The probability that 1269 wrong settings will all have bulges less than B2 is obviously a number fairly close to 1
Back to General Report on Tunny. Contents.