General Report on Tunny
24W Page 135
Therefore various methods of starting the convergence have been suggested. One of these is the method of 'flags'. This consists in comparing every pair of a certain number of rows of the rectangle and scoring these pairs by some scoring system. The resulting scores are entered into a triangle like an American Tournament table and the result examined in order to get a starting pattern for ΔΧ2. This method using scalar products was started by Vergine who had used the method in connection with the Hagelin machine. Later we began entering the flag double entry, making it square and then crudely converging the flag (R2 p 79). The number of rows used varied from 6 to 16 depending to some extent on the type of scoring system used.
The correct scoring system for an assumed value of δ is given by the function ƒ(θ, θ') above. This is troublesome to use in practice and an approximate formula must be used. The usual formula was θθ', so the entries in the flag were simply the scalar products of the pairs of rows. This method is a good approximation if δ is small. (It is the sort of method that a statistician would think of naturally.) When this method is used it is often convenient to divide all entries in the flag by 10 before converging it (giving the results to the nearest whole number).
It might be thought that the scalar product method could be used as a substitute for accurate convergence. However the degree of approximation would be very bad in this case since the pippages involved are much larger. In fact the accurate score of x pips compared with y pips is easily seen to be
(log cosh ½(x+y)p - log cosh ½(x-y)p) natural bans where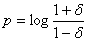 
(i.e. approximately 2δ).
and this is sufficiently close to
log cosh (x+y)δ - log cosh (x-y)δ
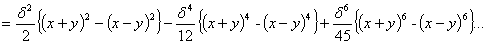
The first two terms can be written
As a rather extreme case, if x = 8, y = 6 and δ = 1/10, the term 2xy δ2 would be 50% too large. So for flag making xy is quite a good approximation (R3 pp 4, 5, 29) if the unit (or 'pippette') is taken as 2δ2 natural bans, i.e. 1 pippette = δ pips. On the other hand, in
Back to General Report on Tunny. Contents.