General Report on Tunny
24Y Page 148
of the test was to key flags (see Chapter 26). For another form of significance test, based on Bayes' theorem, see R3 pp 77, 79. This latter test was applied to 'flag rectangles' (R3 pp 81, 85).
For a theory which connects the score and significance of a complete flag with those of its rectangle, see R4 p 112, R5 pp 17, 21, 90.
24Y OTHER THEORY OF RECTANGLES
(a) Length required to break wheels and rectangles other than 1+2.
The message length required to break all the wheels is about the same as that required for a significant rectangle. Roughly, the score (or double bulge) x of the rectangle (assumed to be 1+2) must satisfy the inequality
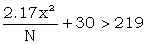 |
|
| assuming the υ terms do not amount to more than 30 decibans. | |
i.e. 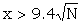 |
|
i.e. since the score on correct wheels is approximately 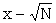 |
|
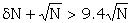 |
|
or 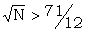 or or 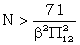 |
|
Observe how sensitive the minimum value of N is to the value of d. The conclusion that the minimum text length required was proportional to (β2π2)-1 was reached by an entirely different method in R1 pp 51, 53. Width d = 21 and π = .2 the minimum N is about 11,000; with d = 28, π = .2 the minimum is about 3000.
For a 4+5 rectangle the condition would be roughly
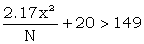 |
||
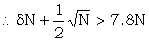 |
(x: δN +  : see R3 p 117) : see R3 p 117) |
|
i.e.  |
||
Incidentally this shows that a 4+5 rectangle would probably be just significant on a shorter text than a 1+2 rectangle if
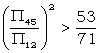 |
i.e. 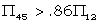 |
This condition was seldom likely to be satisfied and 4+5 rectangles were seldom made. The condition for a 4+5 rectangle to be more decibans up than
Back to General Report on Tunny. Contents.