General Report on Tunny
25A Page 155
A simple check can be applied
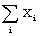 = = 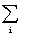 /'s against /'s against 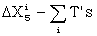 against against 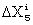 |
 |
||
| = all /'s - all T's | ΔΧ5 | ||
| = (all /'s + all T's) - 2(all T's) | supposed | ||
| = R - 2 norm | all dots |
R is easily measured, being independent of ΔΧ5. The check tests not only the Colossus readings, but, also the subtractions of the norm to find the xi.
Counting T's in ΔD with each character of ΔΧ5 taken in turn to be a cross, all the others being dots, could be done, and in fact originally was done, by actually placing a cross in each position of the trigger in turn; but it is much easier to insert a cross in a fixed position (in practice the last) and allow the wheel to step.
The characters of the wheel are produced in reverse order: (c) shows in detail why this happens.
(c) Why the wheel is obtained backwards.
In such a use of the Colossus wheel trigger it is necessary not to confuse the true wheel, which is of course fixed relative to the cipher, with the wheel trigger, which is deliberately stepped relative to the cipher.
Suppose that the setting of the true wheel relative to the cipher is 1.+ Consider firstly that particular position of the trigger in which its setting is also 1 (so that display and printer read 1): true wheel and trigger now begin in the same place, thus:
 |
The score measured in any position is for that character of the true wheel which is against the cross in the wheel trigger; in this position the last character of the true wheel.
+ 1 is not necessarily 01, for several messages may be used in a wheel-breaking job. The setting for the first message is naturally taken to be 01, though custom sanctions a curious inconsistency, viz. that for Χ1, Χ2 this refers to true settings; for Χ3, Χ4, Χ5, to Δ'd wheels set up on Colossus, whence the (Δ'd wheels) settings 41, 31, 01, 01, 01.
Back to General Report on Tunny. Contents.