General Report on Tunny
25B Page 157
whether it has any significance, and if is so, to evaluate its evidence.
When no evidence other than that provided by the run itself is adduced, a condition for significance is
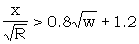 |
|
| where R is the number of places looked at | |
x is sum of the moduli of the scores xi, i.e. the sum of the scores xi ignoring their signs.
x is said to be the "score of the run on its own wheel", for if the run is so completely believed that each positive score is taken as a dot, and each negative score as a cross, the ΔD double bulge is the sum of the moduli.
The test is invariably used when making the initial runs for a new chi wheel.
The run is not necessarily a single run on Colossus, e.g. in attempting to obtain a ΔΧ2 knowing ΔΧ1, ΔΧ2 only, one can do all the runs,
| 3./1.2., 3x/1x2., 3x/1x2., 3./1.2x. |
and find that all fail to satisfy the test, but that if the scores, for each character, of 3./1.2. and 3x/1x2. are added, the resulting run 3+/1.2. is significant. It might otherwise be necessary to combine the three runs 3./1.2., 3x/1x2., 3x/1x2x. Obviously the sum of the two runs will not be more significant unless there is some measure of agreement between them; and in fact it would be bad policy not to do the runs separately.
Note. It is not of course possible to add the x's of two runs to get the x of combined run.
(b) Fundamental decibanning formula.
The formula for calculating the evidence of a significant short wheel-breaking is
decibans per pip = 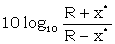 |
where x* is the ΔD score on the correct wheels. (25W(b) and (d)) When the scores of the two or more independent runs are expressed in decibans, they can be added directly.
(c) Decibanning a run on its own wheel.
The score of the run on its own wheel, is generally greater than on the correct wheel, of para (b) for wherever the score against an individual character has the wrong sign, and should diminish the total score, ΔΧ has its
Back to General Report on Tunny. Contents.