General Report on Tunny
25C Page 161
Once a wheel is obtained, runs to improve it are chosen with the aid of the letter count.
At all stages, resourcefulness and experience are needed to deal with abnormal cases.
(d) Some particular runs.
Wheel-breaking almost always starts from ΔΧ1, ΔΧ2: even if it starts from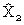 
, the second wheel obtained is usually ΔΧ1.
The short runs then available are
| 3./1.2. | 3x/1x2. | 3x/1x2x | 3./1.2x | |
| 4./1.2. | 4x/1x2x | |||
| 5./1.2. | 5x/1x2x |
The remaining four theoretically possible runs are generally useless.
On a particular at a particular period some of these are better than others, but strong preferences, applied universally, seem difficult to justify, especially when, as ordinarily, the wheels may be inside out.
It is not unusual to do these runs more or less blindly till one of them is found to be significant.
The best run is generally the result of containing two of the above runs, thus obtaining 5=/1=2, 4=/1=2, 3+/1.2. (or 3+/1.2x if the wheels are inside out): indeed if the rectangle is highly significant it may save time to run them thus combined.
If Χ4 or Χ5 is obtained first, the next run is 4=5=1=2 or 4+5.1x2x.
If Χ3 is obtained first, the next run is 4+/3x1x2x.
For the fifth wheel the best letters are as in setting: to attain significance it may be necessary to combine runs. (see R3 p 131, R5 p 106.)
(e) Two-wheel convergence.
If all short wheel-breaking runs fail a conditional rectangle, which is a 2-wheel wheel-breaking run, may be used.
Alternatively it is possible to use a two-wheel convergence i.e. an alternating sequence of short wheel-breaking runs involving two unknown wheels.
Suppose that a ΔΧ1 and ΔΧ2 have been obtained and that although there is no significant run for ΔΧ3, a few characters can be guessed. With this rudimentary ΔΧ3 a short wheel-breaking run e.g. 5JUQ may produce a ΔΧ4 wherewith
Back to General Report on Tunny. Contents.