General Report on Tunny
25E Page 170
(f) Runs to follow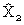 
.
Unfortunately it commonly happens that although the 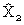run is genuinely significant it is impossible to proceed further.
The strongest run to follow 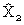is usually (R5 pp 8, 11, 17, 28; 25Y4) Δ Χ1 + ΔZ1 +ΔZ2 + 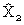= . whose proportional bulge is
 |
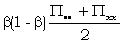The ratio of this to the proportional bulge of 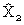is
 |
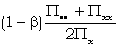which is often considerably less than unity (R5 p 108).
Statistics (R5 pp 98, 105, 106) show that wheel-breaking from a 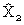start rarely succeeds unless 
.
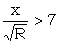Having a significant 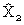the best policy seems to be to set all available messages on 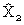(a one-wheel run), not forgetting to span for message slides, strengthening 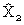, and then trying the wheel-breaking run ΔΧ1 ≠ ΔZ1 + ΔZ2 + 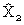= . on each message set. When a ΔΧ1 is obtained the next run 2+/1 is ΔΧ2 + ΔZ2 + ΔΧ1 + ΔΧ2 = . after which ordinary runs are possible.
It is sometimes possible to integrate 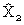i.e. to find Χ2 directly from 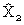, either as a whole, if 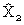is nearly complete, otherwise in strecthes: in the latter case the ambiguities are apt to make the method of doubtful value (See also 26)
It is believed that Jellyfish 4/3/45, broken on 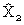, could not have been broken otherwise, (R5 p 52) but ordinarily the advantage of 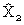over a rectangle is speed. 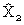is perhaps, most useful as an ancillary method, detecting slides in rectangles, setting rectangles on Χ2, providing a start for convergence, strengthening marginally significant rectangles, acting as a check on dubious characters in Χ2, (X2, ΔΧ2 must satisfy X2 + ΔΧ2 = ).
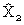(g) Excess of dot or cross in .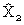
The number of dots and crosses in 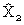may be very far from equal: if the proportional bulge of dots is θ, then ΔZ2 = ., which can be counted in one operation, has a proportional bulge θβπx (25Y1): this has been suggested as a significance test; but it is really more profitable to do 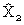properly, for it takes very little time.
(h) X2 + P5 limitation.
Because P5 tends to be dot, this exhibits weakly the characteristics.
Back to General Report on Tunny. Contents.