General Report on Tunny
25Y Page 193
are to be distinguished, multiplied by 23.
In the following table the number of legal wheels is exact: other entries to four figures only.
| Total no. of wheels. |
Δ'd wheels with the correct no. of crosses. |
Legal wheels. |
|
| Χ1 | 2,193,000,000,000 | 271,900,000,000 | 23,314,226,716 |
| Χ2 | 21,43,000,000 | 304,000,000 | 73,241,034 |
| Χ3 | 535,800,000 | 78,320,000 | 14,524,128 |
| Χ4 | 66,990,000 | 19,544,000 | 2,869,568 |
| Χ5 | 8,434,000 | 1,364,000 | 556,416 |
From this table the factor in favour of a wheel because it is spontaneously legal can be calculated. It should be noticed that any supposed ΔΧ wheel corresponds to two Χ wheels or to none, so that e.g. a ΔΧ5, constrained to have the correct number of crosses gains a factor 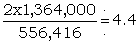 if it is spontaneously legal.
if it is spontaneously legal.
(R5 p 4; for factor given by integration R3 p 30.)
25Y PROPORTIONAL BULGES RELATING TO 
These will all be derived using 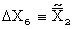 (22D(g))
(22D(g))
The following notation will be used for proportinal bulges
| (. . x) ≡ | β | . . x | denoted | the | P.B. | of | 1 = ., | 2 = ., | 6 = x in | ΔΨ | |
| {. . x} ≡ | δ | . . x | " | " | " | " | 1 = ., | 2 = ., | 6 = x in | ΔD | |
| Πx | " | " | " | " | 2 = x, | ΔP | |||||
| Π.. | " | " | " | " | 1 = ., | 2 = ., | ΔP | Π1+2 | " | " | " | " | 1 + 2 = ., | ΔP |
| θ | " | " | " | " |  = . = . |
||||||
| PB(ΔZ2 = .) | = PB (ΔZ2 + ΔZ6 = .) | |
| = PB(ΔΨ'2 + ΔΨ'6 + ΔΧ2 + ΔΧ6 + ΔP2 + ΔP6 = .) | ||
= PB(ΔΨ'26 + 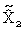 + ΔP2 = .) + ΔP2 = .) |
||
| = βθΠx | ||
| PB (ΔD1 = ., ΔD26 = .) | = ½[{...} + {.xx}] | ||
=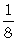 [Π..(... + .xx) + Πxx(xx. + x.x) + Πx.(x.. + xxx) + Π.x(.x. + ..x)] [Π..(... + .xx) + Πxx(xx. + x.x) + Πx.(x.. + xxx) + Π.x(.x. + ..x)] |
|||
Back to General Report on Tunny. Contents.