The King hath note of all that they intend,
By interception which they dream not of.
William Shakespeare. Henry V.
It will be understood from the nature of the Enigma machine that, having been given a replica Enigma by the Poles, complete with a set of rotors and their internal wiring, the task confronting Dillwyn Knox and Alan Turing, the primary British cryptanalysts, was to determine the particular settings of the Enigma machine used to encipher a particular message. Turing and Knox considered three possible methods of attack:
1. Ciphertext-only analysis. This method was later employed in Heath Robinson and the Robinson family of machines and the Colossus series of primitive computers against the FISH traffic encrypted by the Geheimschreiber. It requires ciphertext of a substantial length and so was considered impractical for Enigma traffic which typically consisted of messages of less than 200 characters which is far too little for this type of attack.
2. Discriminant attack. This method, based on an extraordinary German procedural error, was exploited to great effect by the Poles, who achieved the remarkable feat of reconstructing the internal wiring of the rotors by studying the repeated encryption of the three-letter discriminant. It was considered too fragile by Turing and Knox in that the Germans might at any moment change their operational procedures and thereby render useless overnight any machines constructed to assist in the attack. This decision was wise for the Germans did indeed change their procedural methods on May 1st 1940.
3. Probable-phrase attack. This method was based on Turing's realisation that it is possible to exploit the relationship between a known, or guessed, portion of plaintext, called a crib, and the ciphertext. In particular, Turing realised that the relationship between the crib and the ciphertext would preclude some of the stupendous number of ways in which the Enigma machine could have been set up to encipher the plaintext and that accordingly it might be possible to construct a machine to eliminate from consideration many of the ways in which the Enigma could have been set up.
Even if such a machine proved to be practical, would it be possible to find cribs in sufficient quantity? It was not necessary to find a crib for each message, rather, what was required was one crib for each network each day. For once the Enigma settings had been found for that net for that day every message on that net on that day could be deciphered. The Germans would then typically change the settings at midnight and a new crib would have to be found the following day.
But how might cribs be found? German military communications were often expressed in a stereotypical manner so that it was not necessarily difficult to guess a particular phrase that might appear in the message. Further, it might be possible to determine its exact position in the ciphertext by exploiting the property of the Enigma machine which ensured that it never encoded a letter as itself. One very fruitful source was weather reports, for example, the crib used for the first break on D-Day was:
WETTERVORHERSAGEBISKAYA
Now suppose that the ciphertext includes the sequence:
…QFZWRWIVTYRESXBFOGKUHQBAISEZ…
To determine which letter of the crib corresponds to which letter of the ciphertext we slide the crib alongside the ciphertext until we find a correspondence where the same letter does not appear in the same position in the crib and the ciphertext.
|
Q |
F |
Z |
W |
R |
W |
I |
V |
T |
Y |
R |
E |
S |
X |
B |
F |
O |
G |
K |
U |
H |
Q |
B |
A |
I |
S |
E |
Z |
|
W |
E |
T |
T |
E |
R |
V |
O |
R |
H |
E |
R |
S |
A |
G |
E |
B |
I |
S |
K |
A |
Y |
A |
For example, in Figure 1.1, the first S in WETTERVORHERSAGEBISKAYA corresponds to the first S in …QFZWRWIVTYRESXBFOGKUHQBAISEZ…, so we know that this cannot be the correct correspondence because the Enigma machine has the property that it can never encipher a letter as itself.
|
Q |
F |
Z |
W |
R |
W |
I |
V |
T |
Y |
R |
E |
S |
X |
B |
F |
O |
G |
K |
U |
H |
Q |
B |
A |
I |
S |
E |
Z |
|
W |
E |
T |
T |
E |
R |
V |
O |
R |
H |
E |
R |
S |
A |
G |
E |
B |
I |
S |
K |
A |
Y |
A |
So we slide the crib along the ciphertext by one character and again check the correspondences. In this example we again see in Figure 1.2 that the crib is still in the wrong position because a V, E and A appear in both the crib and the ciphertext in the same position.
|
Q |
F |
Z |
W |
R |
W |
I |
V |
T |
Y |
R |
E |
S |
X |
B |
F |
O |
G |
K |
U |
H |
Q |
B |
A |
I |
S |
E |
Z |
|
W |
E |
T |
T |
E |
R |
V |
O |
R |
H |
E |
R |
S |
A |
G |
E |
B |
I |
S |
K |
A |
Y |
A |
So again we slide the crib along, and again we fail to find a possible correspondence because in Figure 1.3 R appears in the crib and the ciphertext in the same position and because in Figure 1.4 W, G and A appear in both the crib and the ciphertext in the same position.
|
Q |
F |
Z |
W |
R |
W |
I |
V |
T |
Y |
R |
E |
S |
X |
B |
F |
O |
G |
K |
U |
H |
Q |
B |
A |
I |
S |
E |
Z |
|
W |
E |
T |
T |
E |
R |
V |
O |
R |
H |
E |
R |
S |
A |
G |
E |
B |
I |
S |
K |
A |
Y |
A |
|
Q |
F |
Z |
W |
R |
W |
I |
V |
T |
Y |
R |
E |
S |
X |
B |
F |
O |
G |
K |
U |
H |
Q |
B |
A |
I |
S |
E |
Z |
|
W |
E |
T |
T |
E |
R |
V |
O |
R |
H |
E |
R |
S |
A |
G |
E |
B |
I |
S |
K |
A |
Y |
A |
In Figure 1.5 we at last see how the crib can be matched to a sequence of cipher text, so there is the possibility that
RWIVTYRESXBFOGKUHQBAISE
is the encryption of
WETTERVORHERSAGEBISKAYA
for one of the 60 rotor orders, 17576 rotor positions, 676 Ringstellung positions and 150,000,000,000,000 stecker swappings.
The question now is which one of the 107,458,687,327,300,000,000,000 possible rotor orders, rotor positions, Ringstellung and stecker swappings was used to encipher the message?
The crib and ciphertext can be paired and numbered as follows:
|
1 |
2 |
3 |
4 |
5
|
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
|
R |
W |
I |
V |
T |
Y |
R |
E |
S |
X |
B |
F |
O |
G |
K |
U |
H |
Q |
B |
A |
I |
S |
E |
|
W |
E |
T
|
T |
E |
R |
V |
O |
R |
H |
E |
R |
S |
A |
G |
E |
B |
I |
S |
K |
A |
Y |
A |
So, if the crib is correctly matched with the ciphertext, we know that some setting of the Enigma will encode R as W and W as R in a particular position which we will call position 1, the Enigma rotor(s) step and then in the next position, which we call position 2, it will encode W as E and E as W, then the rotor(s) step and then in the next position which we call position 3, it will encode I as T and T as I, and so on.

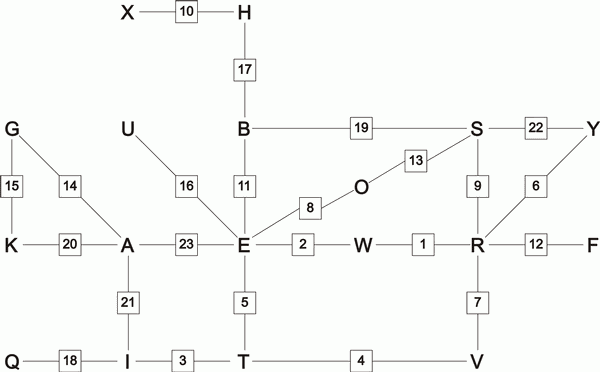
These pairing relationships can be diagrammed as in Figure 1.6. In this diagram the square boxes represent scramblers and the numbers in the boxes represent the positions of the scramblers relative to the position of the scrambler which transformed the first pairing.
Recall that each transformation of one letter into another by the Enigma consists of:
a stecker swapping,
followed by
a scrambler encryption, followed by
another stecker
swapping.
Turing realised that some of these transformations have implications for other transformations and thus can be fed back into themselves to confirm consistency, or, more decisively, to demonstrate a contradiction.
For example, let us test the hypothesis that E is steckered to K. Now consider how E is transformed into A at relative position 23.
If E is steckered to K, K will be input to the scrambler at relative position 23 which will output some other letter v1. Since we know that E transforms into A at relative position 23, we know that A must be steckered to v1.
But if A is steckered to v1, v1 will be input to the scrambler at relative position 21 which will output some other letter v2. Since we know that A transforms into I at relative position 21, we know that I must be steckered to v2.
But if I is steckered to v2, v2 will be input to the scrambler at relative position 3 which will output some other letter v3. Since we know that I transforms into T at relative position 3, we know that T must be steckered to v3.
But if T is steckered to v3, v3 will be input to the scrambler at relative position 5.
Now consider the output of the scrambler at relative position 5 when it receives v3 as its input. Since we know that T transforms into E at relative position 5, we know that the output letter of the scrambler at relative position 5 must be steckered to E.
Suppose, when given v3 as its input, the scrambler at relative position 5 outputs J. By our original hypothesis E is steckered to K, but by our chain of implications E is steckered to J, so in this case E is steckered to both K and J. But the construction of the Enigma does not permit one letter to be steckered to two letters, so E cannot be steckered to both K and J, so our original hypothesis has resulted in an impossible consequence and so must be false.
But now suppose, when given v3 as its input, the scrambler at relative position 5 outputs K. Then by our original hypothesis E is steckered to K, and by our chain of implications E is steckered to K, so in this case E is steckered only to K, thus our original hypothesis has resulted in a consistent consequence and so may be true.
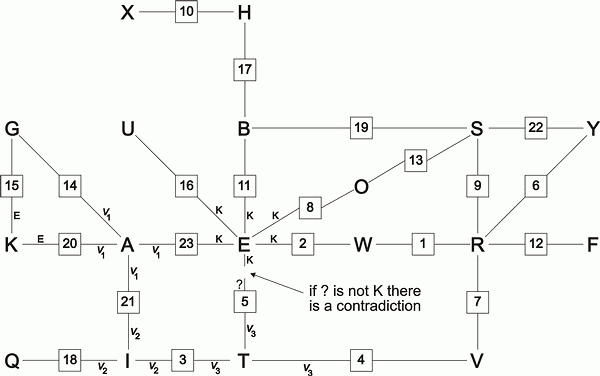
Figure 1.7 shows the hypothesis that E is steckered to K looping back via the chain of implications we have considered.
In general, a steckering hypothesis is consistent if and only if, having returned via some chain of implications to its origin, it implies itself.
Note that by using this method we need loops to feedback into our original hypothesis. When there are four loops in the crib-ciphertext pairing, the feedback imposes a very severe consistency condition, which the vast majority of rotor orders and rotor positions are unable to satisfy.
This concept, of using loops in the crib-ciphertext pairing to test for inconsistencies is the fundamental concept of Turing's probable-phrase attack on the Enigma.
Turing realised that it was possible to represent loops of implications with electrical circuitry and that therefore it was possible to mechanise the search for those rotor orders and positions which satisfy the consistency conditions. The machine which he designed to perform this task is called the Turing bombe.
In other words, the bombe checked whether, with the current rotor order, the current rotor position and any stecker swapping, the crib and ciphertext could be transformed into each other. Thus by successively checking the 60 rotor orders each of 17,576 positions, the bombe performed an exhaustive search of the
107,458,687,327,300,000,000,000
ways in which the Enigma machine could have been set up. By this means it located the needle in the haystack, or perhaps more appropriately, the key to the Third Reich.
Copyright © Graham Ellsbury 1998
Continue to Part 2. Description of the Bombe
Return to The Enigma and the Bombe main page