General Report on Tunny
21 Page 37
---------------------------------------------------------
21 SOME PROBABILITY TECHNIQUES
---------------------------------------------------------
| (a) | Symbols used in symbolic logic |
| (b) | Simple probability notations |
| (c) | Special values of p |
| (d) | Relationship of events |
| (e) | The laws of probability |
| (f) | Some theorems (including Bayes' theorem) |
| (g) | The deciban |
| (h) | Methods of applying the above axioms |
| (i) | Theorem of the weighted average of factors |
| (j) | Theorem of the chain of witnesses |
| (k) | Expected value, standard deviation, variance, distributions |
| (l) | Some special distributions |
| (m) |
Some simple formulae of a non-analytic type, concerning proportional bulges |
| (n) | The general formula for sigma in Tunny work |
| (o) | The statistician's fallacy |
| (p) | The principle of maximum likelihood |
It is assumed that the reader has at any rate an elementary knowledge of probability theory. Therefore the account presented here does not contain many examples but is mainly a list of definitions, notations and theorems. Rigour is deliberately avoided when it would make the account more difficult to read.
(a) Symbols used in symbolic logic.
∨ means 'or'
. means 'and', but the symbol . is often omitted, thus E.F can be written EF (E and F being propositions).
~ means 'not', but we shall write '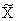
' instead of the usual '~X'.
(b) Simple probability notations.
P(E|H) means the probability of an event E given a hypothesis H. When H is taken for granted we write P(E) simply.
The letter p represents a probability.
The letter o represents odds and is defined by the equation
Back to General Report on Tunny. Contents.