General Report on Tunny
21 Page 38
o =  . The odds of an event E given an hypothesis H are written as O(E|H). Sometimes odds are expressed as a ratio such as '3:2' or '3 to 2'. This means o=3/2. The following phrases are equivalent.
. The odds of an event E given an hypothesis H are written as O(E|H). Sometimes odds are expressed as a ratio such as '3:2' or '3 to 2'. This means o=3/2. The following phrases are equivalent.
'a:b', 'a:b on', 'o = a/b', 'a to b', 'b to a against' etc.
(c) Special values of p.
| 'Certainty' 'Impossibility' 'Evens' |
p=1 or o=∞ p=0 or o=0 p=½ or o=1. |
(d) Relationship of Events.
Two events are 'mutually exclusive' if they cannot both happen. Two events are 'independent' if a knowledge that one is true does not affect the probability of the other one. A number of events is 'exhaustive' if it is certain that one or other of them will happen.
(e) The laws of probability.
| (i) the law of addition of probability | |
| P(E1∨E2|H) = P(E1|H) + P(E2|H) | |
| if E1 and E2 are mutually exclusive. | |
| (ii) the law of multiplication of probabilities | |
| P(E1E2|H) = P(E1|H) P(E2|E1H). | |
| In particular, if E1 and E2 are independent | |
| P(E1E2|H) = P(E1|H) P(E2|H) | |
(f) Some theorems.
| (i) P(E1E2 ... En|H) | |
| = P(E1|H) P(E2|E1H) P(E3|E1E2H) ... P(En|(E1 ... En-1H). | |
| (ii) P(E1∨E2∨ ... ∨En|H) | |
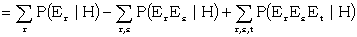 - ... etc., - ... etc., |
and in particular if E1, E2, ..., En are all mutually exclusive, the right hand side can be replaced by 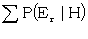 . If E1∨ ... ∨Er is exhaustive the left hand side is 1. Therefore
. If E1∨ ... ∨Er is exhaustive the left hand side is 1. Therefore 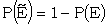 .
.
| (iii) Bayes' theorem. | |
| For various hypotheses Hi (i = 1, 2...) | |
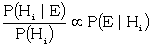 |
The proof of this is simple. For by the law of multiplication of probabilities.
Back to General Report on Tunny. Contents.