General Report on Tunny
23E Page 87
Where Θ is the proportional bulge of ΔΧ2 + Χ2 = .
In practice σ is calculated by supposing Θ = 0, though because Θ may be as great as ½, the error is not always negligible [R5 p. 93].
The exact expressions for A and σ are
| 2=Χ2 : |  ; |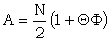
 |
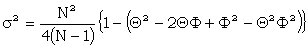| 1=2= Χ2 : |  ; |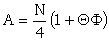
 |
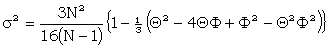where Φ is the proportional bulge of ΔZ2 = ., its expected value being ΘβΠx.
(d) Expected sigma-age of Χ2 limitation break-ins.
The above table para (b) is constructed by finding the expected sigma-ages, WZ (for the last three it is supposed that Θ = 0).
| 1 + 2. | : |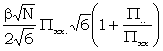 
| |
| 1 + 2 = Χ2x | : |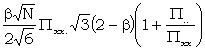 
| |
| 1 = 2 = Χ2 | : |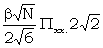 
| |
| 2 = Χ2 | : |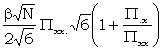 
| |
| 1x2x Χ2x
or 1.2. Χ2x or 1.2. Χ2. |
| : | 
|
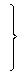
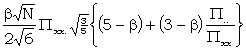
Comparing these
1+2. is better than 1+2. Χ2x
if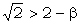 
, i.e. to the nearest
integer [illegible] 28;
1 = 2 = Χ2 is better than 1+2. if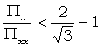 
;
1 = 2 = Χ2 is better than 1+2. Χ2x if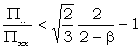 
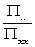is usually small and often negative. The table is devised by supposing it to be 0.1
When Θ is large, the above formulae are unfair to the last three runs, especially to 2 = Χ2.
It may be shown, similarly, but with more algebra, that neither component of 1 = 2 = Χ2, i.e. 1.2. Χ2. or 1x2x Χ2x, can ever be the best run to use. [R0 pp. 40, 44, 107; R1 pp. 5, 9, 27; R5 p. 38; See R5 pp. 13, 29.]
(e) 2 = Χ2.
This is better than its sigma-age would indicate, for it is a one-wheel run. It is at its best for large values of Θ (which may be great as ½), but will never be the strongest run unless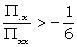 
It takes very little time to run. [R1 pp. 5, 9; see R4 pp. 70, 92].
(f) QTQ.
It is not always known beforehand whether Χ2 limitation is in use. A few links change the limitation frequently (this was common in the
Back to General Report on Tunny. Contents.