General Report on Tunny
23E Page 88
days of P5.) : Sixta is sometimes able to give log information about this (QTQ information).
(g) Tests for Χ2 limitation.
If there is any doubt, the initial run is chosen according to whichever limitation is the more probable, and when the message is set on Χ1 and Χ2, 1 + 2 = . is counted against Χ2 = x and against Χ2 = .. There is an exact formula for the decibannage which this gives in favour of Χ2 limitation, in terms of motor dottage; but commonly a simpler inexact rule is used namely: for Χ2 limitation, the bulge against Χ2x is at least twice the bulge against Χ2..
The earlier rule, that for Χ2 limitation the sigma-age against Χ2 = x should be greater than the sigma-age on the whole text, is grossly biased against Χ2 limitation. [See R4 p. 89. R4 pp. 7, 50, 55, 72.]. If the motor dottage is high it may be impossible to decide whether the limitation is Χ2 until more wheels are set.
(h) 4-letter counts.
When a Χ2 limitation message is set on 1+2, four counts are made against Χ2 = x: 1.2., 1.2x, 1x2x, 1x2.. These confirm that Χ2 is in use and indicate which letter to run for, in particular whether to run for 58U or for / [R5 pp. 38, 71, 80].
(i) C3 = Χ2.
In R5 p. 94 the run 5-4/ = 1x2x Χ2 is suggested, but the evidence is not unbiased.
(j) Χ2 + P5 limitation.
Since P5 → ., this shows the characteristics of Χ2 limitation weekly; the letter 5 is anomalous, being stronger against Χ2 dots [illegible] 74, 87.]
(k) The effect of corruption on 2 = Χ2, 1 = 2 = Χ2.
If there are many corrupt letters replaced by 9ís, the not 99 gadget should be used to ignore these; otherwise, except when Θ = 0, the score may be spuriously enhanced.
It is easy to show that, if a proportion λ of the message consists of corruption 9ís, and the sigma-age of these runs on the incorrupt text is S, then the apparent sigma-age is approximately
| for 2 = Χ2 | : |  |
|
| for 1 = 2 = Χ2 | : | 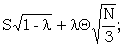 |
Back to General Report on Tunny. Contents.