General Report on Tunny
24E Page 125
24E RECTANGLE SIGNIFICANCE TESTS
(a) In view of the account given in 24X this deals only with tests in practical use.
It is perhaps desirable to stress the distinction between tests for rectangles not converged, i.e. treating the rectangle simply as a run for a wheel 1271 long; and tests for converged rectangles, i.e. using the additional knowledge that the 1271 cells of the rectangle are derived from two wheels 41 and 31 long. The latter are naturally more powerful.
Essentially only one test of each type used operationally; this excludes tests which involve the use of additional evidence.
For rectangles not converged; the square-summing test, or its equivalent the Δ1271 test.
For converged rectangles: Significance Test IV and several simple approximations to it.
(b) Test for rectangle not converged.
If θij is the entry in a cell of a 1+2 rectangle of length N and the depth k (so that N = 1271k) the random
value of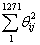 
is N and its variances is
| 2N(k - 1) | (24X(d)) |
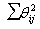is evaluated when making a rectangle on Colossus, by means of a series of
cyclometers which record the number, n(θ), of occurrences of each possible score. Then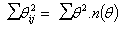 
: the calculation is made foolproof by means of a printed form.
The analogous hand process is possible for a non-Colossus rectangle.
The test is not ordinarily a very powerful one (24), but the following statistics are of some interest.
|
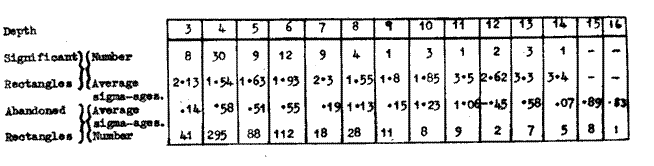
(R1 pp 32, 34, 38, R3 pp 37, 77.)
Back to General Report on Tunny. Contents.