General Report on Tunny
24E Page 126
(c) Δ 1271Test.
Since Δ1271ΔZ12 = Δ1271(ΔD12 + ΔΧ12) = Δ1271ΔD12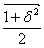
a count of Δ1271Δ Z12 = . is a possible test. It is strengthened if differencing at every multiple of 1271 is included, when it becomes equivalent to the
test (24X(b)) of R2 p 102), for which reason it was discontinued when the cyclometers came into use.
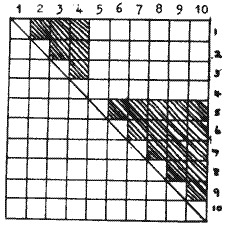
It is however more easily adaptable to the detection of slides. A (half) square is made in which the entry in the cell (m,n) is the number of agreements between the mth and nth stretches of 1271 in ΔZ12. Two stretches in the correct relative positions will show a bulge: two between which there is a slide will show no bulge.
|
In the example depicted there is a slide between the fourth and fifth stretches of 1271 letters. Only the entries in the shaded positions show a bulge. If the slide is near the middle of the fifth stretch, the entries in the fifth row will also show no bulge. |
 |
In fact the expected bulge in a single cell is only about σ, so that long texts are required: the method is not in current use.
The counts can easily be made on Robinson using a cipher tape or any kind of Thurlow Tape. Two copies are required; if their lengths are consecutive multiples of 1271, the whole test can be made very quickly without stopping the machine.
If a slide is suspected, it may be investigated by similar runs with an artificial slide between stretches from different parts.
(See R3 pp 77, 82, 92, R4 pp 71, 82, 122.)
(d) Significance test for converged rectangles.
The standard test for a 1+2 rectangle is
 |
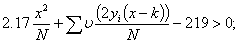Back to General Report on Tunny. Contents.