General Report on Tunny
24F Page 127
the left hand side being the decibanage in favour of significance, where yi is the modulus of the score of a character and Σ is extended over both wheels, 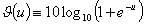 and is tabulated, k is controversial (see 24X (e))
and is tabulated, k is controversial (see 24X (e))
For other rectangles 219 should be replaced by 3.01(w1 + w2 - 1) + 5, where w1, w2 are the two wheel lengths.
The formula is believed to provide a normally reliable condition for the essential correctness of the rectangle wheels. Ordinarily, though not always on all links, this implies that wheel-breaking can be completed, though it cannot be guaranteed, for it depends on supporting messages and on ΔP characteristics in impulses not used for the rectangle.
The formula has been criticised because Σν is tedious to calculate and varies but little. Approximation have been suggested.
 |
(for messages 10168 long: R3 p 5). |
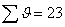 i.e. i.e. 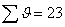 |
(based on a perversattitude to decibans: R4 pp 111, 115) |
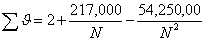 i.e. i.e. 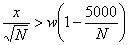 |
|
| (Too optimistic for small N: used by the computers). | |
An empirical formula for Σν as a function of N in a marginally significant rectangle would have been preferable.
In practice everyone assumes that Σν is about 20-30, being greater for short messages and that if 2.17 x2/N, the LEADING TERM, is more than 200 or much less than 180 it is unnecessary to calculate the ν terms. (see R2 p. 15, R4 pp 40, 111, 117).
24F CONDITIONAL RECTANGLE
This means a rectangle in which scores are counted only at places of Z where some fixed condition is satisfied.
e.g. in a cell of the 3+4x/1x2x rectangles the entry is
(the number of places where ΔZ3 + ΔZ4 = x, ΔD1 = x, ΔD2 = x) minus
(the number of places where ΔZ3 + ΔZ4 = ., ΔD1 = x, ΔD2 = x).
The convergence is identical with that of an ordinary rectangle.
Almost the only conditional rectangles used are 3+4x/1x2x, 4+5/1+2, 4+5/1x2x (see next section 24G)
Back to General Report on Tunny. Contents.