General Report on Tunny
24x Page 139
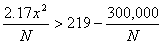 |
This gives, to a sufficient approximation,
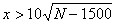 |
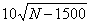 was therefore tabulated.
was therefore tabulated.
Some time later (R4 pp 111, 117) another alternative was suggested, also based on an empirical consideration of ν terms. Unfortunately it was not based on a careful study of the statistics about ν terms available by that time. The sum of the ν terms for N = 8 x 1271 were examined empirically, since the sample for this text length was considerable (R3 p 95). It was found that this sum could be approximated by the expression
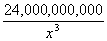 ± 3.6 decibans. ± 3.6 decibans. |
This enabled one to say (with only a small probable error) how many decibans up or down any rectangle of this length would be, given X. By 1945 there were probably sufficient statistics to obtain an empirical simplification for all values of N, but this was never done.
(d) Significance test for a rectangle not worked on - the square summing text.
By a 'significant test for a rectangle not worked on' we mean a test which depends only on the numbers in the 1271 cells of the rectangle and not on any convergence of the rectangle for comparison of the rows. Such a test is the one referred to as significance test 0, which amounts roughly to summing the squares of all the 1271 entries in the rectangle. (This test appeared in the 'Black File' at an early date.) Naturally such a test cannot be as powerful as tests which can be applied after the rectangle is converged but occasionally a result is obtained enabling one to forecast that the rectangle will be significant when converged.
Let the entry in the cell (i,j) of the rectangle θij. Then the function required in 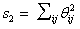 . There is a gadget on Colossus which counts the number of occurrences of each values of |θij| when producing a rectangle, so that s2 can be calculated without difficulty.
. There is a gadget on Colossus which counts the number of occurrences of each values of |θij| when producing a rectangle, so that s2 can be calculated without difficulty.
A test that can be applied even before the rectangle is made is the so-called 'slide and significance test'. Leaving aside the part of this test that deals with the detecting of slides it can be shown that this test is equivalent to square summing. The test consists in counting
Back to General Report on Tunny. Contents.