General Report on Tunny
24X Page 140
Δ1271ν(ΔZ12) = . for ν = 1, 2, ..., k-1, using a message of length N=1271k stuck with the end running straight on to the beginning. This method of sticking enables the text length used for each of the (k-1) counts to be equal to N. The result is that if the scores for ν = 1, 2, ... (k-1) are added together and the result is called X then every pair of letters in ΔD at a distance which is a multiple of 1271 will have an opportunity of contributing either 2 or 0 to N. The total number of such distinct pairs of letters is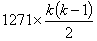 
so that 
is defined as the bulge B of the test. It is reasonable to suppose that the value of B (if δ = 0) is 0 and that its S.D. is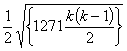 
. Both of these assertions are true, though the proofs are not entirely trivial. Further it is clear that
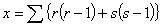
summed over all cells of the rectangle, where r is the number of dots and s is the number of crosses in a typical cell. If we now remember that r + s = k, r - s = θij,
, 
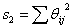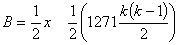
it follows that
.
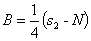This is the connection between the square-summing test and the 'Slide and significance test'. It is implicit in all this that the expected value of s2 is N and that its S.D. is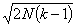 
.
The distribution of s2 or B is really of Χ2 type but it is near enough to a normal distribution for most practical purposes.
In order to see how strong the test is we may argue as follows: The number of comparisons is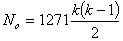 
and the P.B. for a given value of δ, in each comparison is δ2. Thus the expected sigma-age is 
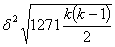. For example if k = 8 the expected sigma-age is 187δ2. If δ = .1, which is sufficient for the significance of the converged rectangle, the expected sigma-age would be 1.9. If δ = .15 the expected sigma-age is 4.2, so highly significant rectangles are liable to be picked out quite well. One might be tempted to reject all rectangles whose sigma-age on the test was negative, but although this should not often happen if the rectangle is a good one, it also does not often happen anyway and the factor against the rectangle being significant is not at all large.
Back to General Report on Tunny. Contents.