General Report on Tunny
24X Page 141
In order to estimate this factor, the simplest method is as follows:
Let sigma-age observed be s.
Let sigma-age expected for a given value of δ be s1.
| Then | 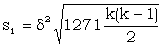 |
and the factor in favour of a particular value of δ rather than δ = 0 is, if we assume σ independent of δ,
 |
|
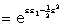 |
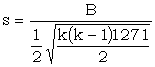 |
| Therefore natural banage is | 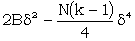 |
|
 |
||
 say. say. |
||
The factor in favour of δ > δ0, rather than δ < δ0, assuming a uniform prior distribution for δ for positive δ (and no chance if δ < 0), is
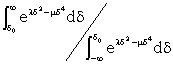 |
|
| If s2 = N, k = 3, δ = .08 this reduces to | |
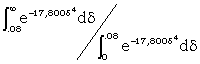 |
|
| = .15. |
Thus with N = 10168 a zero score on the significance test implies a factor of about 6 against the rectangle being significant.
The original discussion of 'significance test 0', given in the black file, makes no assumptions about distributions and is a direct application of Bayes' theorem. We proceed now to give an account of this with simplification and correction of the original argument. It is not assumed that the length N of the message is necessarily a multiple of 1271.
Let us assume some definite value of δ and suppose that the depth of the rectangle in a particular cell is k. Then the probability that there will be an entry of Θ in the cell (where Θ and k are integers
Back to General Report on Tunny. Contents.