General Report on Tunny

24X Page 142

of like parity) is

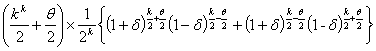and therefore the factor in favour of this value of δ rather than δ = θ is
 
  = sechkδ' . cosh (θδ'),
  where ,

and is very close to δ in all practical cases. The natural banage from all the cells together is thus
 
 
  where ,

Now E(s2) = N, E(s4) = 3kn, E(s6) = 15k2n, ... if δ = 0 and N = 1271k so, if δ2N < 200, a sufficiently good approximation is
 

Observe that we cannot neglect the term in δ4 since E(s2 - N) = Nkδ2, so the expected value of the second term is about half of that of the first term if δ is small. If we write s4 = 3kN there is still a small discrepancy between the natural banage obtained here and that obtained before. This discrepancy is due to the assumption (see R4 p 122) that σ is independent of δ. A more interesting remark is that the present method shows that the evidence of the value of s4 should be taken into account. The 'maximum likelihood' value of δ is
 
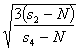though this is itself liable to a large S.D. which can be estimated. Larger values of s4 given smaller values of δ so the previous formula lays too much stress on the higher entries in the rectangle.


(e) Significance tests for rectangles which have been crudely converged.

Let the double bulge on /1+2 on a message of length N, against the correct wheels be x2. (We assume no slide - otherwise the phrase 'correct wheels' becomes ambiguous.) If a crude convergence is done, starting with one of the correct wheels (say ΔΧ1), then a result will be

< previous

next >

Back to General Report on Tunny. Contents.

Back to The Enigma and the Bombe main page

Home