General Report on Tunny
24Y Page 150
whether the Δwheels were relatively inside out.) The rival good positions can then be scored by a more accurate method. Before we had time to work out the correct wheel-sliding table a cruder method was used. This cruder method is to evaluate
 |
Denote the decibanage of a typical character of one wheel
by x, so that its odds of being a dot are xy = 10x/10 and probability
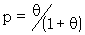. Let p = ½ (1 +
Π). Let the probability of having an x in a cell of the first wheel be
px if the character is a cross. Then the probability of having
an x if the character is a dot is θpx. Denote by x', θ',
p'x' the corresponding functions for the second wheel. Then the
probability of seeing an x opposite an x' if the relative position of the
two wheels is correct and they are not relatively inside out is
| ½(px px' + θpx θ'p'x') | |
| and if it is wrong | |
| ½ px(1 + θ) ½ p'x'(1 + θ') | |
Therefore the factor obtained from one pair of entries in favour of the slide being correct is
 |
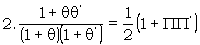The factor obtained from the complete comparison is
 |
In order that this formula should not be misleading, it is necessary to allow for competition, because the correct wheel may have very good slides against itself. A table exists for accurate wheel-sliding with pip value 2/3 deciban (See R1, 97).
(d) Setting two messages in depth on Chi 1 and Chi 2.
Closely related to significance test 0 is the problem of attempting to set two messages in depth on chi 1 and chi 2 before either rectangle is converged: (R1, 75; R3, 28, 35). In order to show how close the relationship is, the problem can be attacked in the following way. Let each of the 1271 different relative settings of chi 1 and chi 2 be tried out. For each of
Back to General Report on Tunny. Contents.