General Report on Tunny
24Y Page 151
these let significance test 0 be applied. Let θ, θ' denote typical entries in the separate rectangles, then the expression considered is Σ(θ + θ')2. This is equal to Σθ2 + Σθ'2 + 2Σθθ'. The first two terms are independent of the particular selection amongst the 1271 theories. Thus the method is equivalent to scalar multiplication. If the length of the messages are 1271k and 1271k' with P.B. of ΔD12 = dot of δ and δ', then the proportionate bulge of ΔZ12 and ΔZ12', in a particular cell, is δδ' if the rectangles are correctly set relatively. The number of comparison is 1271kk' so the expected sigma-age is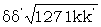 
. In order that this should exceed 3 it is necessary that either 
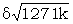or 
should exceed 10. Thus it is impossible for two rectangles to be set by Significance Test 0 (i.e. when unconverged), unless at least one of them would be significant according to Significance Test IV (i.e. when converged). The sum may nevertheless, of course be significant according to Significance Test IV, but 1271 separate convergences are impracticable. This scalar product method is an approximation to the theoretically correct method of comparing the two rectangles by means of the wheel-sliding table treating them as wheels 1271 long (R3, 35).
Back to General Report on Tunny. Contents.